![]() Le prestazioni e le caratteristiche dei compound termicamente conduttivi sono molto migliorate rispetto a quelle dei primi prodotti apparsi sul mercato oltre quindici anni fa. La diffusione di questi materiali è avvenuta soprattutto in ambito elettrico ed elettronico, dove le esigenze di progetto sono particolarmente stringenti sia dal punto di vista prettamente termico, sia sul versante della trasformazione. Gli sviluppi successivi hanno interessato diverse aree tematiche, innanzitutto le formulazioni, che sono diventate sempre più complesse per assicurare elevati valori di conduttività termica, uniti ad altre caratteristiche come l’autoestinguenza.
Le prestazioni e le caratteristiche dei compound termicamente conduttivi sono molto migliorate rispetto a quelle dei primi prodotti apparsi sul mercato oltre quindici anni fa. La diffusione di questi materiali è avvenuta soprattutto in ambito elettrico ed elettronico, dove le esigenze di progetto sono particolarmente stringenti sia dal punto di vista prettamente termico, sia sul versante della trasformazione. Gli sviluppi successivi hanno interessato diverse aree tematiche, innanzitutto le formulazioni, che sono diventate sempre più complesse per assicurare elevati valori di conduttività termica, uniti ad altre caratteristiche come l’autoestinguenza.
Le difficoltà tipiche dello stampaggio a iniezione, per esempio il riempimento di spessori sottili e l’estrazione, sono state gestite lavorando sulla fluidità delle resine e sulla morfologia delle cariche. Anche i prezzi, inizialmente piuttosto elevati, sono stati ottimizzati grazie al miglioramento dell’efficienza dei processi produttivi, all’economia di scala e alla concorrenza. Nonostante questo, però, alcune difficoltà di impiego ancora oggi limitano la fiducia di progettisti e tecnici. Il primo ostacolo è di natura prestazionale, dato che la capacità di gestire il calore di questi materiali non è ritenuta soddisfacente in diverse applicazioni. Altre incertezze sono legate ai vincoli imposti dal colore naturale (nero o bianco) e alla fragilità meccanica, dovuta all’elevatissimo quantitativo di cariche disperse nella matrice, e all’aspettativa di vita utile di manufatti così poco convenzionali.
Se buona parte di questi limiti sono oggi gestibili a livello di formulazione del compound, resta da eliminare una serie di inconvenienti generati da una progettazione molto spesso affrontata considerando i compound come se fossero alluminio da pressofusione. Proprio su questo punto è necessario lavorare per trasformare i materiali termoconduttivi in una scelta vincente.
Polimeri conduttivi: vantaggi e difficoltà
Le soluzioni termoplastiche oggi disponibili sul mercato prevedono l’adozione di cariche ceramiche per i gradi elettricamente isolanti e di grafite per quelli elettricamente conduttivi. In entrambi i casi l’obiettivo è quello di ottenere il miglior compromesso tra un’elevata conduttività termica e caratteristiche meccaniche accettabili. Alla base di questo scenario si collocano i gradi più semplici, caricati con ossidi metallici e dotati di una conduttività termica isotropica sensibilmente inferiore a 4-5 W/mK. Dal contesto si distinguono le formulazioni più estreme, a base di grafite o nitruro di boro, le cui prestazioni termiche possono essere oltre cento volte superiori a quelle della resina di base, con conduttività spesso superiori ai 20 W/mK.
Tabella 1 Conduttività termica indicativa e densità di alcuni materiali
| Conduttività termica (W/mK) | Densità (g/cc) | ||
|---|---|---|---|
| Allumina | 36 | 3,95 | |
| Grafite | 70 | 2,1 | |
| Hex-BN | 29 | 2,1 | |
| Alluminio pressofuso | 100 | 2,7 | |
| Zama | 100 | 6,7 | |
| Polimero | 0, 2 | 1 | |
| Laticonther 62 GR/70 (sul piano) | 27 | 1,76 | |
| Laticonther 62 GR/70 (perpendicolare al piano) | 5 | 1,76 |
Ricordando che l’alluminio da pressofusione ha una conduttività termica di circa 90-100 W/mK e che un polimero tal quale si attesta invece attorno a 0,1-0,2 W/mK (tabella 1), è evidente come la sostituzione del metallo con i compound sia una strada potenzialmente percorribile.
Come già discusso e riconosciuto in più ambiti tecnico-scientifici, la maggiore conduttività del metallo diviene ridondante qualora il passaggio determinante nel trasporto di calore sia la trasmissione all’aria più che la conduzione nel radiatore, come per esempio avviene in regime di convezione naturale. Detto questo, da cosa nascono i problemi che rendono complessa l’adozione dei materiali sintetici più performanti?
Anisotropia e orientamento
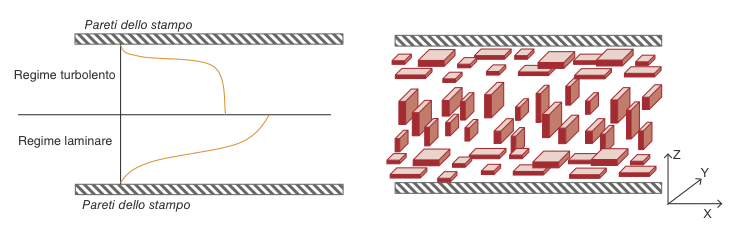
La caratteristica comune tra la grafite e il nitruro di boro esagonale è la struttura planare. Queste cariche si presentano come sottili lamine – o flakes – caratterizzate da un fattore di forma piuttosto elevato, generalmente compreso fra 6 e 10 (tabella 2). È evidente come questa morfologia sia alla base di almeno due fenomeni di grande importanza. Innanzitutto, il piano della laminetta sarà la direzione preferenziale lungo la quale il calore tende a spostarsi. Un trasferimento di calore in direzione perpendicolare al piano della lamina richiederebbe infatti una conduttività altrettanto elevata. In secondo luogo, è plausibile che si verifichi un forte orientamento delle stesse durante lo stampaggio a iniezione a causa degli sforzi di taglio presenti nel polimero fuso iniettato in cavità.
Tabella 2 Fattore di forma di alcuni tipi di cariche e conduttività stimata
| Aspect ratio | K (W/mK) | |
|---|---|---|
| Allumina | 3,5 | 36 |
| Ossido di magnesio | 3 | 23 |
| Nitruro di boro | 7 | 29 |
| Grafite | 6-6 | 75 |
I fattori appena descritti si traducono in due effetti macroscopici, ossia:
• una forte anisotropia della conduttività termica, che risulterà molto più elevata lungo la direzione di avanzamento del fuso e in corrispondenza del massimo orientamento dei flakes termoconduttivi;
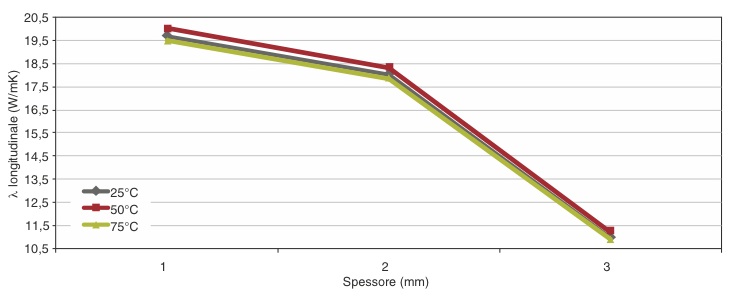
• una dipendenza del valore medio di conduttività dallo spessore della parete riempita. A pareti sottili si associa una conduttività più elevata lungo il piano che perpendicolarmente a esso. Per spessori crescenti si osserva invece un progressivo avvicinamento dei due valori a un terzo valore intermedio tra i due e corrispondente a una condizione di orientamento casuale delle lamine.
Alla luce di queste evidenze è ragionevole adottare un unico valore di conduttività termica per compound caricati con filler ceramici pressoché sferici. Al contrario, ignorare anisotropia e orientamento dei filler più performanti può essere fuorviante e far decadere un progetto potenzialmente valido, avendo trascurato i vantaggi che questi aspetti potrebbero garantire.
Dispersione del calore per irraggiamento
Il calore che può essere disperso per irraggiamento è legato alla temperatura dell’ambiente e della superficie che emette una radiazione mediante un parametro proprio del materiale, l’emissività (ε):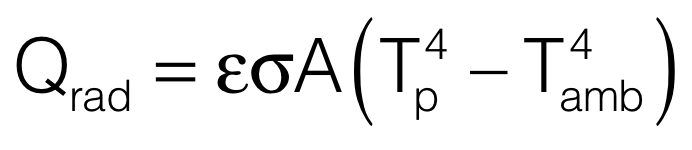 Molti dei manufatti realizzati in alluminio pressofuso non vengono normalmente sottoposti a lavorazioni superficiali che ne migliorino le capacità di irraggiamento. Se consideriamo l’alluminio non trattato notiamo che la sua emissività è inferiore a 0,2 anche per superfici molto ossidate e che raggiunge 0,5 solo dopo anodizzazione. Per i materiali termicamente conduttivi questo valore è decisamente superiore senza alcun trattamento: si misura, infatti, un valore prossimo a 0,87 per le superfici nere dei materiali caricati con grafite e a 0,75 per quelle dei caricati con ceramiche. La differenza è evidente, e conferma il vantaggio di cui i manufatti in compound termoconduttivo possono fregiarsi qualora si riesca a trasferire calore per irraggiamento.
Molti dei manufatti realizzati in alluminio pressofuso non vengono normalmente sottoposti a lavorazioni superficiali che ne migliorino le capacità di irraggiamento. Se consideriamo l’alluminio non trattato notiamo che la sua emissività è inferiore a 0,2 anche per superfici molto ossidate e che raggiunge 0,5 solo dopo anodizzazione. Per i materiali termicamente conduttivi questo valore è decisamente superiore senza alcun trattamento: si misura, infatti, un valore prossimo a 0,87 per le superfici nere dei materiali caricati con grafite e a 0,75 per quelle dei caricati con ceramiche. La differenza è evidente, e conferma il vantaggio di cui i manufatti in compound termoconduttivo possono fregiarsi qualora si riesca a trasferire calore per irraggiamento.
Questo aspetto è spesso trascurato in fase di progettazione proprio perché si approccia il problema con le classiche soluzioni dei metalli. I manufatti andrebbero invece concepiti in modo che il fattore di vista (o view factor) della geometria preveda una buona parte delle superfici esposte verso l’esterno e non reciprocamente affacciate. Quanto invece si osserva oggi è che i tipici dissipatori sono costituiti da ampie superfici alettate, che tuttavia finiscono con l’irraggiarsi a vicenda. Calcoli alla mano, un radiatore in compound termicamente conduttivo correttamente disegnato e ottimizzato può arrivare a cedere oltre il 50% del calore da smaltire per irraggiamento. Ecco perché far guidare le scelte progettuali dal semplice valore di conduttività termica può rivelarsi drammaticamente fuorviante.
Gli strumenti da utilizzare
Il problema della corretta progettazione con compound termicamente conduttivi è quindi molto più complesso di quanto normalmente affrontato con i metalli. Si devono infatti gestire non solo la migliore emissività e l’irraggiamento, ma soprattutto la conduttività termica reale del materiale, che abbiamo appurato essere legata all’orientamento delle cariche. Per spessori superiori a 4-5 mm si misura un progressivo avvicinamento dei valori di conduttività sul piano e trasversale a esso: la ridotta differenza suggerisce anche in questi casi la possibilità di adottare un valore unico per semplificare i calcoli. Resta comunque una grande approssimazione, specialmente nel caso di geometrie a basso spessore in cui l’orientamento di grafite o nitruro di boro esagonale è molto forte (figure 1, 2 e 3).
 Il problema della conduttività termica appena descritto richiama per molti aspetti quello dell’anisotropia delle caratteristiche meccaniche nei compound rinforzati, per esempio con fibra di vetro e carbonio. Nel caso di questa ampia famiglia di materiali la questione è stata affrontata e brillantemente risolta da tempo, fornendo ai tecnici strumenti di calcolo avanzati, operanti con il metodo degli elementi finiti. I software moderni riescono a valutare preventivamente l’orientamento dei rinforzi e a stimare con grande accuratezza i valori locali del modulo elastico che determina tanto la robustezza del manufatto, quanto i ritiri differenziati alla base di deformazioni e stabilità dimensionale.
Il problema della conduttività termica appena descritto richiama per molti aspetti quello dell’anisotropia delle caratteristiche meccaniche nei compound rinforzati, per esempio con fibra di vetro e carbonio. Nel caso di questa ampia famiglia di materiali la questione è stata affrontata e brillantemente risolta da tempo, fornendo ai tecnici strumenti di calcolo avanzati, operanti con il metodo degli elementi finiti. I software moderni riescono a valutare preventivamente l’orientamento dei rinforzi e a stimare con grande accuratezza i valori locali del modulo elastico che determina tanto la robustezza del manufatto, quanto i ritiri differenziati alla base di deformazioni e stabilità dimensionale.
I risultati di queste simulazioni numeriche permettono di produrre fin da subito manufatti dimensionalmente corretti, la cui resistenza meccanica viene ottimizzata in fase progettuale, riducendo così il time-to-market e i costi di sviluppo. È possibile esportare il medesimo approccio ai compound termoconduttivi?
La struttura di R&D e co-design di Lati (Vedano Olona, Varese) ha cominciato a lavorare sui compound termicamente conduttivi all’inizio degli anni 2000. Molte problematiche sono state via via affrontate e risolte per permettere agli utilizzatori di sfruttarne al meglio le proprietà. Oggi la sfida è quella di estendere l’impiego di questi materiali innovativi anche ad applicazioni decisamente più impegnative, dove la quantità di calore da gestire è di molte decine di watt, per esempio l’illuminotecnica basata sui potenti LED COB o i dispositivi utilizzati in ambito elettronico e automotive. Tutti scenari, questi, in cui potenze spesso esuberanti vanno gestite in concomitanza a elevate temperature ambientali e all’esigenza di assoluta affidabilità. Situazioni simili possono essere affrontate solo se non si prescinde dall’ottimizzazione delle prestazioni e del design di dissipatori e alloggiamenti con un preciso ruolo dal punto di vista termico.
Un esercizio di progettazione
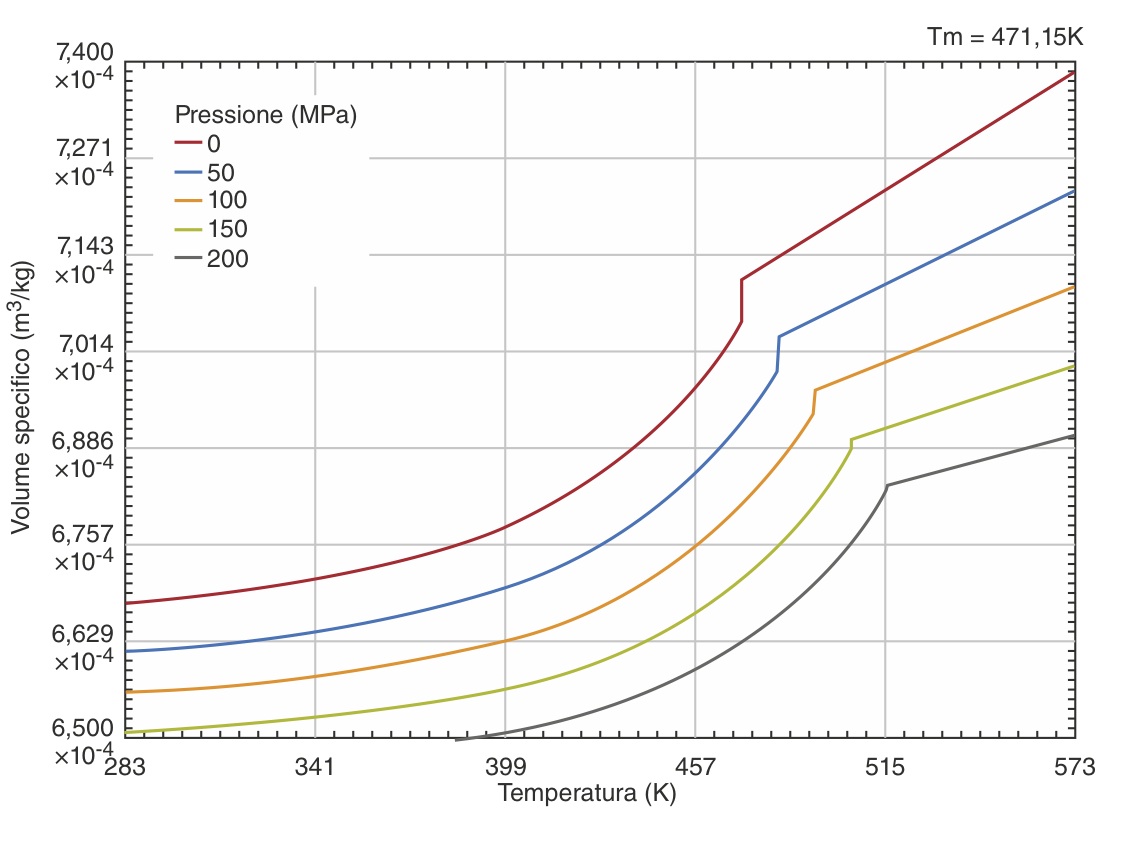
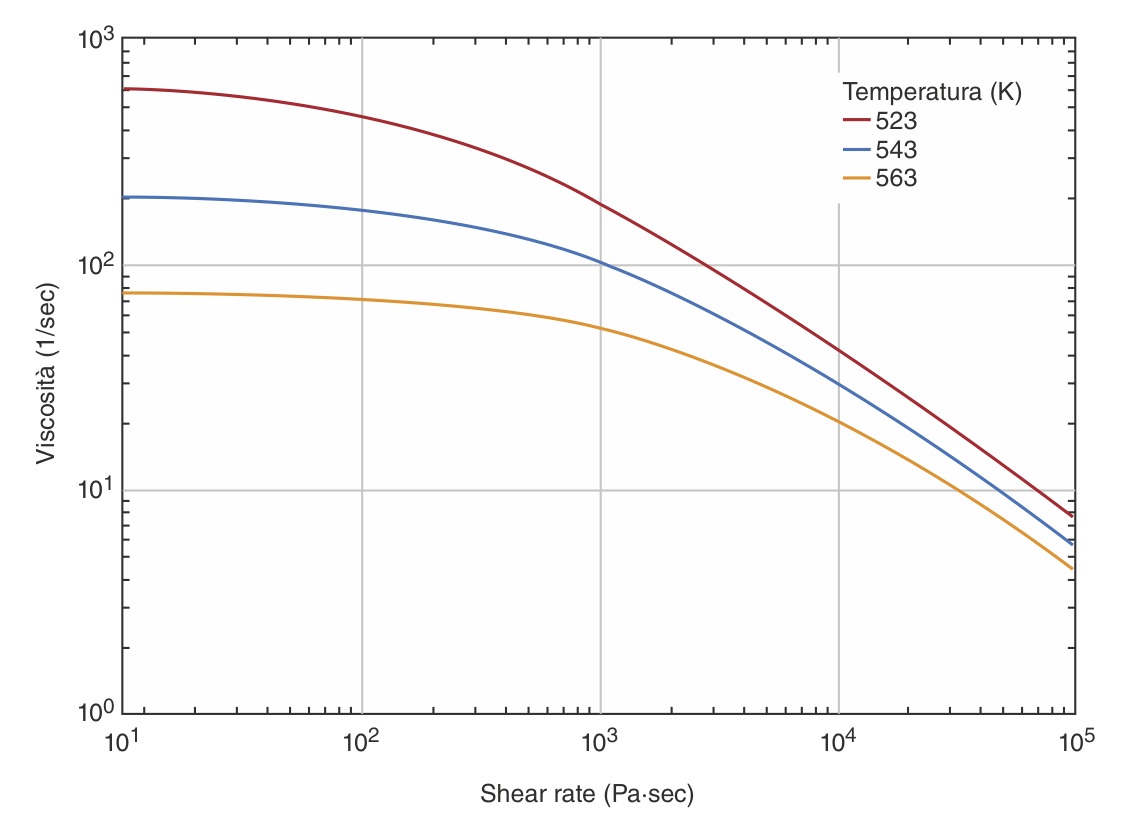
Immaginiamo di adottare un approccio simile a quello riservato alla progettazione con i materiali plastici strutturali anche per la realizzazione di un dissipatore di calore da produrre impiegando un compound caricato con elevate percentuali di grafite. Una prima valutazione di fattibilità è ricavabile ricorrendo ai fondamenti della fisica del trasporto di calore, valutando le prestazioni della geometria semplificata e del materiale mediante il calcolo dei numeri adimensionali significativi (Prandtl, Nusselt, Reynolds e Grashof), con cui stimare il coefficiente di scambio termico (hconv) per il regime di convezione naturale. Questo parametro è indispensabile per la corretta soluzione dell’equazione di scambio termico: Il passo successivo consiste nel tentare di simulare il comportamento reale del materiale termoconduttivo tenendo conto dell’efficienza del filler su tutta la geometria, punto per punto. Per ottenere questa fondamentale matrice di dati si deve disporre, in primo luogo, dell’informazione inerente alla disposizione delle particelle grafitiche nel manufatto. È quindi necessario eseguire una simulazione di riempimento dello stampo utilizzando la caratterizzazione reologica completa del compound termoconduttivo, ossia curve PVT (figura 4), curve di viscosità (figura 5), dati fisici e meccanici.
Il passo successivo consiste nel tentare di simulare il comportamento reale del materiale termoconduttivo tenendo conto dell’efficienza del filler su tutta la geometria, punto per punto. Per ottenere questa fondamentale matrice di dati si deve disporre, in primo luogo, dell’informazione inerente alla disposizione delle particelle grafitiche nel manufatto. È quindi necessario eseguire una simulazione di riempimento dello stampo utilizzando la caratterizzazione reologica completa del compound termoconduttivo, ossia curve PVT (figura 4), curve di viscosità (figura 5), dati fisici e meccanici.
Lati dispone di diversi prodotti così descritti all’interno della banca dati del software Moldex3D, tra questi per esempio i gradi basati su poliammide 6 caricata con grafite al 50 e 70%. Nel software di calcolo, le particelle di grafite vengono approssimate a flakes circolari aventi un fattore di forma pari a 10. Si tratta di una semplificazione accettabile, considerata la tipica geometria della grafite realmente dispersa nel compound. L’orientamento delle cariche viene calcolato su ogni elemento insieme al valore medio locale e alla percentuale di particelle disposte lungo tale direzione. Tutte le componenti del tensore “orientamento” vengono raccolte in colonne di dati messe a disposizione dell’utente.
A questo punto, è possibile operare sulle colonne di dati per assegnare a ogni elemento una conduttività termica locale, a sua volta scomposta lungo le tre direzioni principali. A ciascuna delle tre componenti – che chiameremo kx, ky, kz – si assegna un valore stimato ricorrendo alle indicazioni del tensore orientamento. Come riferimento viene preso il massimo valore di conduttività termica assegnabile al compound nel caso di orientamento ottimale lungo un singolo asse: per il Laticonther 62 GR/70 tale valore limite è stato rilevato sperimentalmente ed è pari a circa 27 W/mK. Si ottiene così – in modo grossolano ma affidabile – una nuova matrice che descrive l’anisotropia della conduttività termica elemento per elemento.
Ogni elemento della discretizzazione FEM risulta ora dotato di un set di parametri che considerano le reali prestazioni termiche locali, trasferibili nella scheda materiale a esso associata. Potenzialmente, è come se ogni elemento fosse costituito da un materiale a sé stante, dotato di un comportamento termico differente da tutti gli altri. Naturalmente, è necessario evitare una sovradescrizione del fenomeno: si ottengono già ottimi risultati riducendo il numero di “materiali indipendenti” a un centinaio circa. Una volta importate queste informazioni in un software di calcolo termico si può simulare accuratamente il comportamento anisotropo del materiale, imponendo le condizioni al contorno previste dal progetto: flusso termico, temperature e irraggiamento in regime stazionario o in transitorio.
Un metodo efficace
Il metodo finora descritto è stato sperimentato nel corso di alcuni progetti particolarmente impegnativi dal punto di vista prestazionale. In questi casi era richiesta la gestione di molte decine di watt di potenza termica e la qualità del risultato fornito dalle FEA era di estrema importanza. Le simulazioni hanno confermato quanto ipotizzato, ossia che l’orientamento delle particelle grafitiche è fondamentale per ottimizzare il trasporto del calore. Facendo riferimento a un dissipatore come quello rappresentato nelle figure 6-10 la sperimentazione ha confermato come la particolare disposizione della grafite nelle alette dei dissipatori possa contribuire concretamente alla dispersione del calore, favorendone il passaggio lungo lo sviluppo verticale delle stesse. L’orientamento del filler sulla base dei dissipatori potrebbe invece contrastare il trasporto di calore verso le alette, ed è quindi da preferirvi una disposizione più casuale delle particelle conduttive.
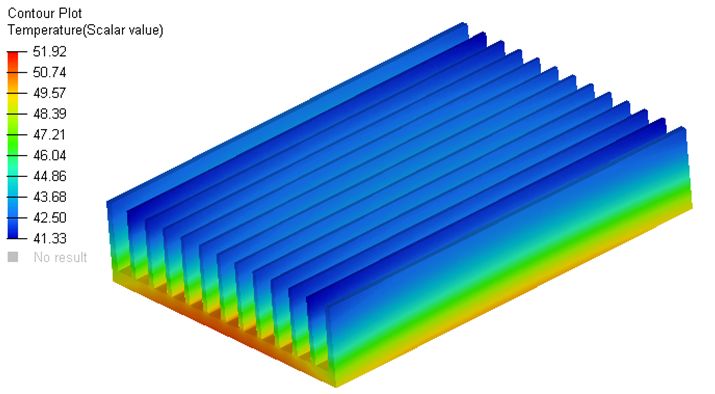
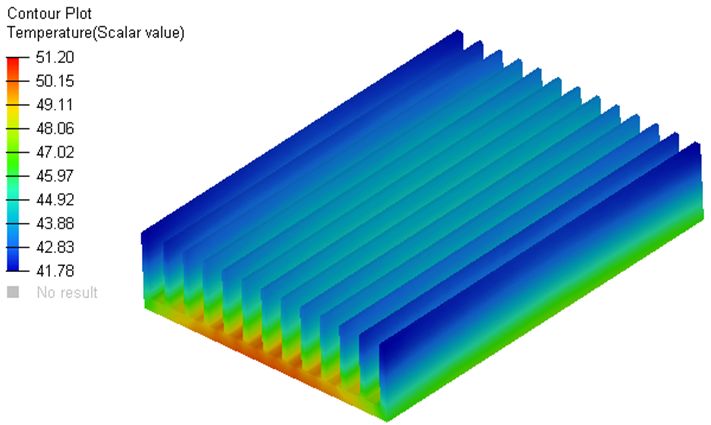
Queste indicazioni possono teoricamente tradursi in accorgimenti specifici su geometria del manufatto, posizione e tipo del punto di iniezione, velocità e cinetica di riempimento. Per esempio, laddove si desideri un trasporto termico efficiente in una direzione specifica si può pensare di adottare spessori relativamente sottili (1-2 mm); per ottimizzare lo scambio di calore in direzione trasversale è invece opportuno scegliere spessori superiori a 4-5 mm).
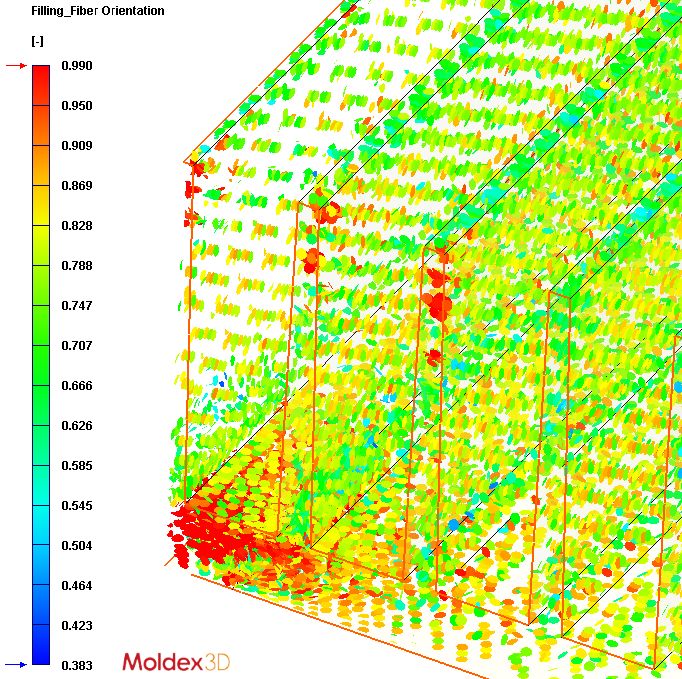
Per il radiatore in discussione (gentile concessione di Electromagnetica) è stata calcolata una differenza di temperatura di oltre 5 °C sulle alette a favore del modello anisotropo, confermando come l’approccio omogeneo isotropo sottostimi – in questo specifico caso – le reali prestazioni del materiale nella geometria proposta. Orientamento della carica e irraggiamento sono stati gli elementi indispensabili che hanno permesso di progettare un radiatore di grandi dimensioni (oltre 50 x 75 cm), completamente in tecnopolimero e capace di dissipare oltre 500 watt.

 Infine, lo studio comparato dei risultati ottenuti con l’approccio isotropo e quello anisotropo si è rivelato utile anche per confermare il valore “unico” di conduttività termica, ovvero quello da adottare per semplificare i calcoli qualora si desideri prescindere dall’anisotropia della carica.
Infine, lo studio comparato dei risultati ottenuti con l’approccio isotropo e quello anisotropo si è rivelato utile anche per confermare il valore “unico” di conduttività termica, ovvero quello da adottare per semplificare i calcoli qualora si desideri prescindere dall’anisotropia della carica.
Un approccio ragionato
La messa a punto del metodo di calcolo descritto è stata decisamente laboriosa, soprattutto per la preparazione degli strumenti informatici con cui gestire le informazioni e tradurle in un formato compatibile con i software FEM commerciali impiegati in Lati. La migliore gestione del problema richiede più passaggi, dato che per ogni progetto deve essere effettuato prima il calcolo del coefficiente di scambio termico (h), poi una simulazione fluidodinamica di riempimento impiegando una caratterizzazione reologica completa del compound, quindi la manipolazione dei dati di orientamento del filler e per finire una o più simulazioni termiche.
I risultati ottenuti lasciano intravedere una concreta possibilità di approcciare l’adozione dei compound termoconduttivi con strumenti che ne descrivano adeguatamente le prestazioni reali, e che pertanto gettino le basi per un impiego moderno e ragionato degli stessi. Se tale strada verrà percorsa anche dai produttori di software ufficiali non possiamo che attenderci conferme ancora più entusiasmanti.





